近期,欧洲杯买球完全官网吴冯成课题组与美国马里兰大学凝聚态理论中心的Haining Pan博士, Ming Xie博士和Sankar Das Sarma教授合作,在半导体摩尔超晶格中拓扑量子物态的理论研究上取得新进展,相关工作以“Topological Phases in AB-Stacked MoTe2/WSe2: Z2 Topological Insulators, Chern Insulators, and Topological Charge Density Waves”为题,发表在国际著名物理学术期刊Physical Review Letters(《物理评论快报》)上。武汉大学和武汉量子技术研究院为文章的共同署名单位,吴冯成教授是文章的独立通讯作者。
两个相同或相似的二维材料堆叠起来,层间的相对转角或晶格常数差异会导致一个具有长周期的摩尔超晶格。这一超晶格为调控量子物态提供了全新的手段。近年来,具有摩尔超晶格的转角双层二维材料体系涌现出了许多新奇的物理效应,例如由转角调控的平带、超导态、关联绝缘态、量子反常霍尔态等。此前,吴冯成与合作者从理论上提出了利用半导体摩尔超晶格进行量子模拟,包括:(1)基于半导体异质结对强关联Hubbard模型进行量子模拟[F. Wu et al., Phys. Rev. Let. 121, 026402 (2018)];(2) 基于半导体同质结对拓扑能带模型 (Kane-Mele 模型) 进行量子模拟 [F. Wu et al., Phys. Rev. Let. 122, 086402 (2019)]。这一系列理论预言陆续获得了实验验证。2020年3月份,Nature杂志发表了两篇背靠背的实验文章 [Nature 579, 353 (2020); Nature 579, 359 (2020)] ,同时报道了在半导体摩尔超晶格中实现了对Hubbard模型的量子模拟。
2021年, 美国康奈尔大学的Jie Shan与Kin Fai Mak实验小组在异质结MoTe2/WSe2中[T. Li et al., Nature 600, 641 (2021)], 发现了在空穴填充数为1(2)时,由外加电场调控的莫特绝缘态(能带绝缘体)到量子反常霍尔态(量子自旋霍尔态)的转变。该实验展示了在同一体系中,通过改变电子填充数与外加电场,可以实现种类丰富的量子物态。令人意外的是,该实验在异质结(而非同质结)中实现了拓扑量子物态,因而引出了许多值得研究的新问题。
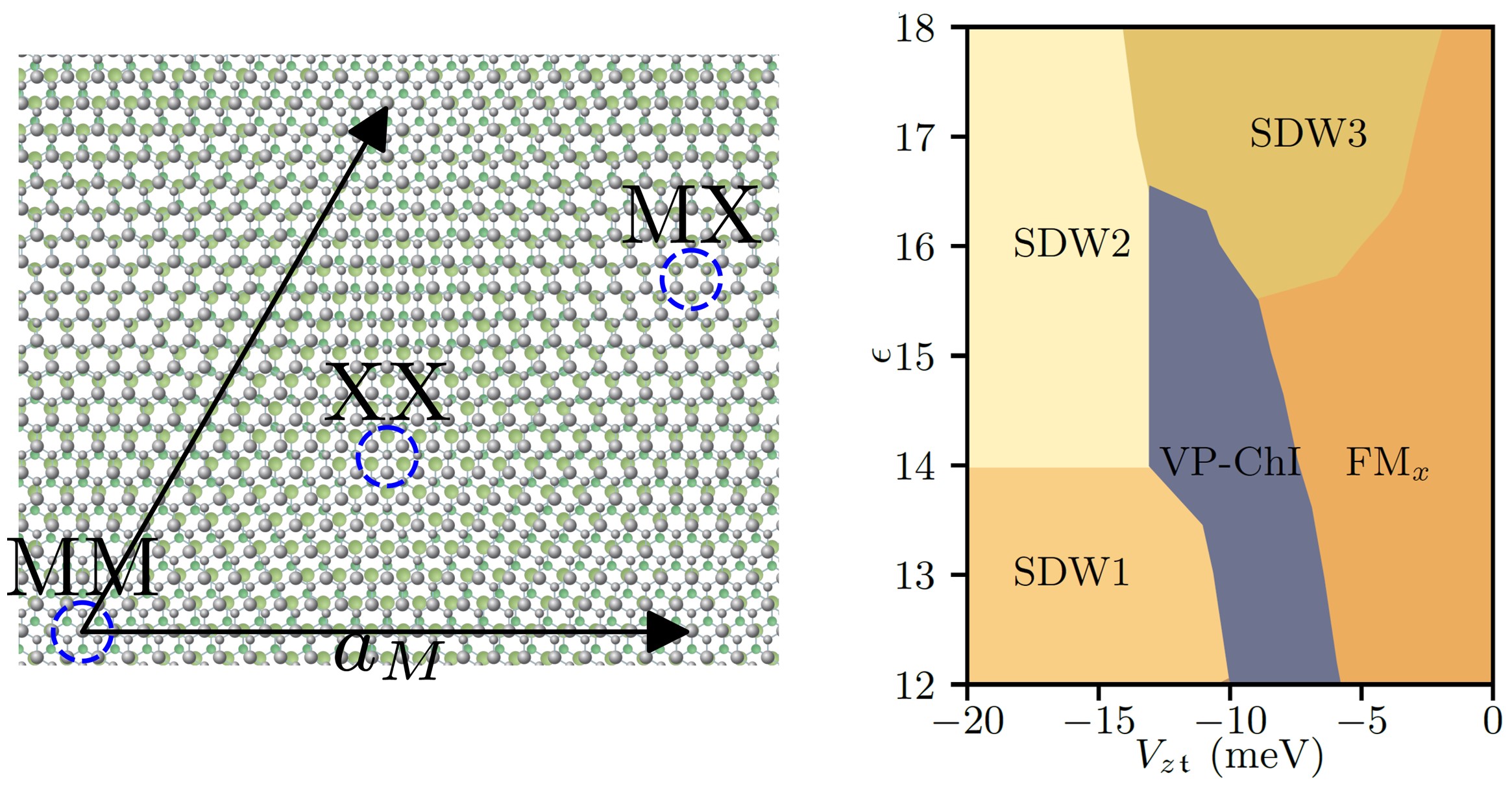
图1 MoTe2/WSe2摩尔超晶格(左图)中,由多体相互作用导致的ν=1量子相图(右图)。
基于前期研究积累,吴冯成教授与合作者针对MoTe2/WSe2体系展开理论研究,构建了有效的摩尔能带模型,并利用平均场方法处理电子间的多体相互作用,绘制由电子填充数、相互作用强度、外加电场等调控的量子相图。研究发现,(1)当空穴填充数为2时,量子自旋霍尔态的绝缘能隙由多体相互作用打开;(2)当空穴填充数为1时,有一系列相互竞争的量子物态,包括能谷极化态、能谷相干态、磁性密度波态等,其中能谷极化态在一定的外加电场范围内是量子反常霍尔态;(3)当空穴填充数为分数2/3时,电荷密度波态在外加电场调控下也可以成为量子反常霍尔态。研究结果不仅为实验现象提供了理论解释,而且预测了新的量子物态,例如拓扑电荷密度波。此项工作为调控低维拓扑量子物态提供了重要的理论支撑。
文章链接: https://doi.org/10.1103/PhysRevLett.129.056804